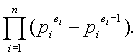The RSA Cryptosystem
RSA History
- Invented in 1977 by Rivest, Shamir, and Adleman.
- One of the first public-key system
- Based on the difficulty of factoring large integers.
Problems With Secret-Key Cryptosystems
- Up until now all of our system have been symmetric, or secret-key, cryptosystems.
- There are many of these systems that work very effectively, but the main disadvantage is that the two individuals that want to communicate, Alice and Bob, have had to secretly exchange the key either in person or over a secure line.
- If they already have a secure line at their disposal then it seems that they would send that message over that secure line and would have no need for a cryptosystem.
- Public-Key Systems attempt to solve this problem
Public-Key Cryptosystems
- The idea is to create a cryptosystem in which it is computationally infeasible to determine the decryption rule given the encryption rule.
- If we can create such a system then we can publish the encryption rule for everyone to see, this is our public-key.
- When sent a ciphertext, then we use our secret-key to decrypt.
- A good way to think of this is that Alice places an object in a metal box, and then locks it with a combination lock left there by Bob. Bob is the only person who can open the box since only he knows the combination.
Note: Public-Key Cryptosystems are also not void of problems. A public-key cryptosystem can never provide unconditional security because an opponent upon seeing a ciphertext, can encrypt each possible plaintext until this ciphertext is obtained.
Definition
- ek is called a one-way trapdoor function if it is easy to compute but hard, computationally, to invert, unless the user possesses secret information that permits easy inversion of ek.
Some Number Theory (first in order to set up for the RSA system)
- Zm* = {aÎ
Zm : gcd(a, m) = 1} is group under multiplication called the prime residue group.(recall that we used this group in the Affine Cipher.)
- The Euler phi-function, f
, for every nÎ
Z+, is defined as f
(n) is equal to the number of positive integers less than n that are relatively prime to n.
- Example: f
(2) = 1, f
(3) = 2, f
(4) = 2, f
(5) = 4, and f
(6) = 2
- It is clear that |Zm*| = f
(m).
More Number Theory
- The Fundamental Theorem of Arithmetic tells us that every integer greater than 1 is a prime or a product of primes.
- Hence, if mÎ
Z+ such that m > 1, then
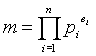
where the pi’s are distinct primes, n is the number of distinct primes, and ei>0 is the power of the associated prime.
Personal Note: This next result gives us a way to compute the value of f
(m).
Theorem(Phi Calculation) (WRITE ON BOARD)
- Suppose
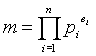 as above, then f
(m) =
as above, then f
(m) = 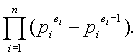
Proof
- First look at the case were m = p, where p is a prime. Then f
(p) = p – 1, since all the numbers 1,…,p, except p, are relatively prime to p.
- Now let us compute when m = pn. Think of the numbers, 1, …, pn.
- Which of these is divisible by p? Clearly the answer is p, 2p, 3p, …, pn.
- Thus, every p numbers we get a number that is divisible by p.
- There are pn/p = pn-1 such numbers, which are all not relatively prime to pn.
- Hence, f
(pn) = pn – pn-1.
- It turns out that f
respects multiplication in Z. (I will not prove)
- Then if m = a product of primes to powers, then f
(m) can be broken up into f
(p1e1)…f
(pnen), but each of these can be calculated using the result 2 lines above and we are done.
Recall: Corollary to LaGrange’s Theorem that says: If G is a finite group and aÎ
G. Then a|G| = e.
Recall: Fermat’s Little Theorem which states:
If p is a prime and aÎ
Z+ such that p does not divide a, then ap – 1 º
1 (mod p)
Personal note: now we can present the RSA system.
The RSA Cryptosystem
- The RSA cryptosystem is defined by P = C = Zn, and
K = {(n, p, q, a, b) : n = pq, p, q prime, ab º
1 (mod f
(n))}.
For k = (n, p, q, a, b), we define
ek(x) = xb mod n
and dk(y) = ya mod n, where x, yÎ
Zn and n and b are public.
- This system is based on two ideas:
- A fast algorithm for finding a random prime number of a prescribed size is known.
- No fast algorithm for a factorization of a large number into a product of primes is known.
Verification That Encryption and Decryption are Inverse Operations
- We will show that dk(ek(x)) = x for any kÎ
K and xÎ
P.
Proof
- Since ab º
1 (mod f
(n)), then we have that ab = tf
(n) + 1 for some integer t³
1
- Suppose that xÎ
Zn*, then we have dk(ek(x)) = (xb)a mod n
(xb)a º
xtf
(n) + 1 (mod n) (substituting for ab)
º
(xf
(n))tx (mod n) (rules of powers)
º
(x|Zn*|)tx (mod n) (since |Zn*| = f
(n))
º
(1)tx (mod n) (by the corollary to LaGrange’s Theorem)
º
x (mod n)
- Now, suppose xÎ
Zn\Zn*.
- From the Phi Calculation Theorem, f
(n) = (p – 1)(q – 1).
- It is true from number theory(the Chinese Remainder theorem) that
xab º
x (mod pq) if and only if xab º
x (mod p) and xab º
x (mod q).
- If x º
0 (mod p), then xab º
x (mod p).
- If x is not congruent to 0 (mod p) then
xab º
xtf
(n) + 1 (mod p) (substituting for ab)
º
(x(p – 1))t(q - 1)x (mod p) (substituting for f
(n))
º
(1)t(q - 1)x (mod p) (Fermat’s Theorem)
º
x (mod p)
- Similarly, we can redo steps c and d for q. This yields:
xab º
x (mod p) and xab º
x (mod p).
- Hence, xab º
x (mod pq).
4) Therefore, dk(ek(x)) = x.
An RSA Cryptosystem can be created as follows:
1. Select at random two large prime numbers p and q (say >100 digits each).
2. Compute n = pq.
3. Select an integer b that is relatively prime to f
(n).
4. Compute a º
b-1 mod f
(n) (multiplicative inverse).
5. Publish pair P = (b, n) as RSA Public Key.
6. Keep pair S = (a, n) as RSA Secret Key.
7. ek(x) = xb (mod n) to encrypt.
8. dk(y) = ya (mod n) to decrypt.
Note: For all of these steps there are algorithms that will accomplish the given task in polynomial time. This means that there are algorithms such that the time of computation is no more than a polynomial function of the problem size.
Security
- The security of the RSA cryptosystem is based on the idea that no algorithm is able to factor an integer with more than 100 digits in a feasible amount of time.
- There is no polynomial time solution to factorization of an integer.
- Most factoring algorithms have computational time that is an exponential function of the problem size. As we know, exponential functions grow much faster than polynomial functions.
RSA example:
This is a small insecure example of the RSA system.
In practice, random primes are chosen of 100 digits or more.
- We select the primes p = 41 and q = 59. (In implementation the computer picks two random primes of prescribed size).
- Now we compute n = (41)(59) = 2419.
- Since f
(n) = (p – 1)(q – 1), from the Phi Computation Theorem, then
f
(2419) = (40)(48) = 2320. We need to select an integer b that is relatively prime to 2320. Any such integer will work. In particular b = 3 works, because gcd(3, 2320) = 1.
- Now we need to compute a. a º
b-1 (mod 2320)
º
3-1 (mod 2320) º
1547 (mod 2320)
Thus, a = 1547. We can check this by computing ab mod f
(n) which is suppose to equal 1. (1547)(3) (mod 2320) = 1, so a and b check out.
- The public-key is the pair (3, 2419).
- The secret-key is the pair (1547, 2419).
- Encryption is accomplished by ek(x) = x3 (mod 2419).
- Decryption is accomplished by dk(y) = y1547 (mod 2419).
Subexample: If the message ‘goodbye’, corresponds to the value 516, then Alice would encrypt this message by:
ek(516) = 5163 (mod 2419) = 991, this would be sent to Bob
Oscar is in trouble unless he can factor 2419 into two primes and then calculate a. To get the plaintext back, Bob uses his secret key:
dk(991) = 9911547 (mod 2419) = 516. And he now knows that Alice has said ‘goodbye’.
Note: if all possible messages correspond to a different integer, then there are only 2419 different possible messages.
Conclusion:
- There are many other secret-key and public-key cryptosystems out there.
- I hope that I have given a good introduction into some of the more basic systems and one of the not so basic ones.
- For more information on anything that I have spoken on I have attached a list of references to get a good start into understanding cryptography or you may approach me personally and I can lead you in the direction of cryptography readings.
References:
Adamek, Jiri. Foundations of Coding; New York: John Wiley & Sons, Inc., 1991.
Bogomolny, Alexander. Euler Function and Theorem; 2001.
<http://www.cut-the-knot.com/blue/Euler.html>.
Cook, Diane J. Lecture 23: Encyption; 2001.
<http://www-cse.uta.edu/~cook/aa/lectures/l23/l23.html>.
Hardy, Darel W. Information Integrity and Security; Colorado State University, 1999.
<http://hardy.math.colostate.edu/m460/>.
Koblitz, Neal. Algebraic Aspects of Cryptography; Springer-Verlag Berlin Heidelberg, 1998.
Stinson, Douglas R. Cryptography: Theory and Practice; CRC Press, Inc., 1995.
Using Matrices for Cryptography; 2000. <http://www.route66isp.com/~limax/Cryptography.pdf>.
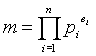
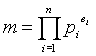
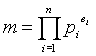 as above, then f
(m) =
as above, then f
(m) =